Data visualisation, ou comment ne pas rater le dinosaure dans vos données
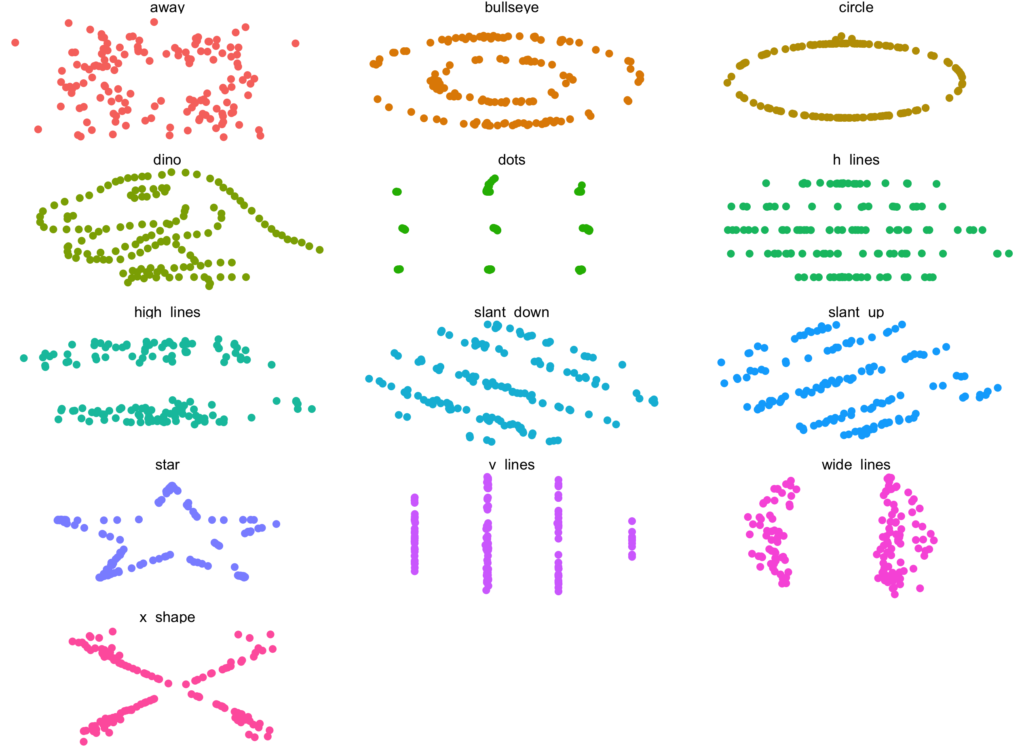
La légende (ainsi que wikipédia) raconte que le statisticien Francis Anscombe a créé 4 jeux de données (le “Quartet d’Anscombe”) afin de contredire l’idée communément admise selon laquelle “les calculs numériques sont exacts, mais les graphiques sont approximatifs” (“numerical calculations are exact, but graphs are rough”). D’après lui, les graphiques peuvent “nous aider à percevoir et à apprécier certaines grandes caractéristiques des données et nous permettre de regarder au-delà de ces caractéristiques pour voir ce qu’il y a d’autre”.
C’est ce qu’il va démontrer dans son article “Graphs in statistical analyses” (Anscombe, 1973), et que nous allons expliquer ici.Il construit 4 jeux de données (“dataset”) qui vont servir sa démonstration. Voici à quoi ressemblent les jeux de données :
Chaque jeu de données (A, B, C, D) comprend 11 observations. Chacune de ces observations a 2 valeurs, qu’on appelle variables X et Y. On pourrait imaginer qu’il s’agisse de 11 observations qu’un chercheur a recueilli sur 4 terrains différents. Par exemple, cela pourrait représenter un chercheur en biologie végétale qui rentre dans une parcelle de terrain A; il choisit 11 coquelicots au hasard dans cette parcelle et il en mesure la hauteur (X) et la largeur (Y). Il recommence l’opération dans une autre parcelle (B) en prenant les mesures de hauteur et largeur de 11 nouveaux coquelicots, et ainsi de suite jusqu’à obtenir la hauteur et largeur de 44 coquelicots, soit 11 observations avec 2 mesures provenant de 4 endroits différents. Maintenant, imaginons que ce chercheur en biologie veuille comparer la hauteur et la largeur des coquelicots de la parcelle A avec ceux de la parcelle B. Il va donc comparer ces 2 jeux de données :
Il se retrouve donc avec 22 observations à comparer, plus précisément 11 observations à comparer avec 11 autres. Le chercheur a des limites mnésiques et de perception qui l’empêchent de faire cette comparaison “de tête”. Il va donc essayer de résumer ces données, grâce à des indicateurs statistiques. Il peut donc calculer, par exemple, la hauteur moyenne des coquelicots de la parcelle A et celle des coquelicots de la parcelle B puis comparer ces 2 moyennes. Ainsi l’information sera résumée à 2 indicateurs, rendant la tâche de comparaison beaucoup plus facile que de comparer 22 observations. Pour calculer la moyenne, le chercheur doit prendre les hauteurs des 11 coquelicots de la parcelle A, les additionner entre elles, puis diviser le résultat par le nombre d’observations, donc 11. On obtient donc le calcul suivant :
Il répète l’opération pour les hauteurs de coquelicots de la parcelle B. Il se rend alors compte que la moyenne est la même, c’est à dire 9. Il s’intéresse alors à la largeur des coquelicots, et calcule la moyenne de la largeur des coquelicots de la parcelle A puis B. Il trouve là encore une égalité entre les deux jeux de données. Pour la parcelle A comme pour la B, la moyenne de la largeur des coquelicots est de 7,5. Il va alors essayer de comparer les coquelicots de A et B grâce à d’autres indicateurs, comme l’écart-type, qui est en quelque sorte la moyenne des écarts à la moyenne. Par exemple, on sait que la hauteur moyenne des coquelicots de la parcelle A est 9. La première observation de coquelicot de la parcelle A est 10 de hauteur. Ici, la première observation a donc un écart à la moyenne de 1. La troisième observation donne une hauteur de 13, donc l’écart est alors de 4 par rapport à la moyenne 9. En calculant l’écart de chaque observation avec la moyenne de cet échantillon, on peut ensuite estimer la « dispersion » des résultats en calculant un moyenne des écarts observés à la moyenne. C’est cela qu’on appelle l’écart type. Dans notre cas, l’écart type de la hauteur des coquelicots de la parcelle A est de 3,3. Cela signifie qu’en moyenne, la hauteur de ces coquelicots se disperse autour de la moyenne plus ou moins 3,3. Le chercheur a une multitude d’autres indicateurs statistiques à sa disposition, comme la variance, le coefficient de régression, l’équation de la ligne de régression, la somme des carrés…
Le chercheur procède à ces calculs, sur les 4 jeux de données. Voici ce qu’il obtient :
Ici les statistiques sont formelles: les 4 jeux de données sont équivalents. Leurs indicateurs sont les mêmes. En ne se basant que sur les statistiques, bien qu’elles soient justes, le chercheur concluerait que les jeux de données sont équivalents. En résumant les données par l’utilisation des statistiques, le chercheur a ainsi “caché” une partie de ces données pour n’en garder que des indicateurs.
C’est à ce moment qu’intervient le besoin de visualiser les données pour ne pas passer à côté d’informations importantes cachées dans le jeu de données.
Réaliser un graphique permet de visualiser les données d’une autre manière, en “un coup d’œil ». Ici on va créer un nuage de points. Chaque point aura pour coordonnées X et Y les valeurs X et Y des jeux de données. En reprenant notre exemple de biologie végétale, c’est comme si on affichait la relation entre la hauteur et la largeur des coquelicots des différentes parcelles. Voici à quoi cela ressemble.
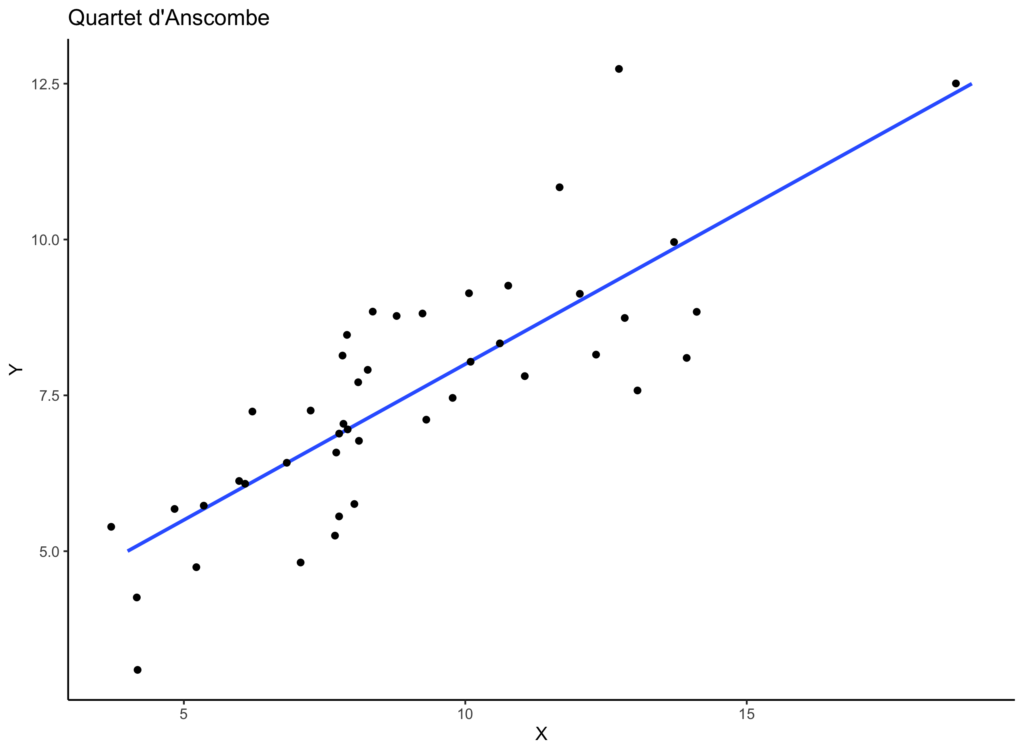
Ici rien n’est particulièrement notable. On voit simplement qu’il y a une relation positive entre X et Y, autrement dit la hauteur et la largeur de nos coquelicots.
Si on affine le graphique en le démultipliant pour chaque jeu de données dont proviennent les observations (autrement dit on montre cette relation entre hauteur et largeur, mais pour chaque parcelle), on obtient ceci :
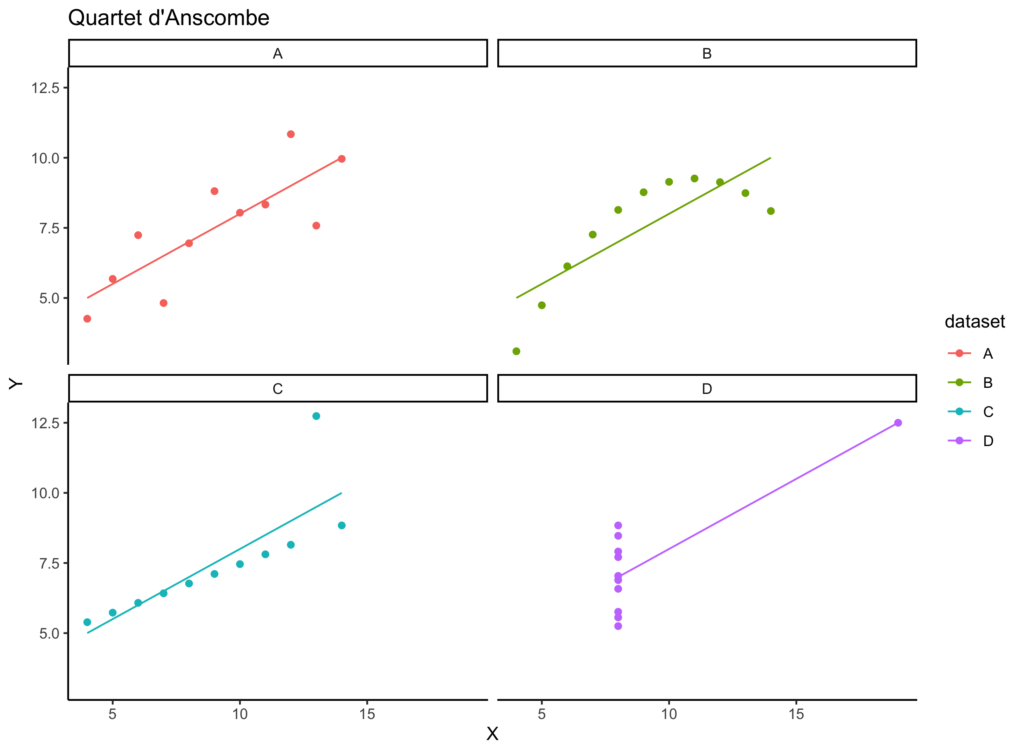
C’est seulement maintenant que l’on se rend compte que les jeux de données ne se ressemblent pas du tout, donc qu’ils ne sont pas équivalents, contrairement à ce que laissaient penser les statistiques. La démonstration est ainsi faite que la visualisation de données peut être un atout majeur dans un processus d’analyse de données. Ne pas l’avoir fait aurait ici conduit à des erreurs d’interprétations très importantes sur les jeux de données, jusqu’à en tirer des conclusions fausses.
Les jeux de données utilisés ici ont été créés pour le besoin de la démonstration, mais leur caractère factice n’enlève rien à la pertinence de la démonstration. Montrer les données permet de révéler la structure qu’il peut y avoir dedans, des patterns reconnaissables. D’autres chercheurs ont reproduit des jeux de données comme ce fameux Quartet d’Anscombe. Par exemple, l’image utilisée en tête de cet article contient d’autres jeux de données qui ont les mêmes indicateurs statistiques (moyennes, écarts types, etc) que ceux du Quartet d’Anscombe (oui, même le dino).
Maxime Péré
UX Researcher
19 mai 2021











